Prof’s Ancient Egypt

Extracts from a New Book
"The Pyramid Builder's Handbook"

by

Derek K Hitchins

Contents

Introduction

Work needed to Raise Great Pyramid, Tier-by-Tier

Time Taken per Tier

Numbers of Men Directly Employed in Hands-On Work

Rates of Setting Stone in Place

Rates of Setting Stone during corvée

Parallel Pathways on Ramps

How long did it all take?

Conclusion

Introduction

If you look up any good book on the pyramids it will give you basic information on each pyramid's height, base lengths, volume, weight, orientation, etc. For instance, the Great Pyramid has a volume of 2,583,283 cubic metres, height 146.59 metres, base of 230.33 metres, a mass of 7 million tonnes, and so on.

Using these figures, it is possible to work out other factors like the rate of laying stones, in tonnes per hour, given a build time generally assumed for the Great Pyramid to be 20 years. The figure often quoted is 89 tonnes per hour, which would be an average over the full 20 years - pretty tremendous, but does the average conceal even higher peak rates?

Such average figures can be quite misleading, especially when you realize that putting the top stones in place must have taken a lot more work than putting on a base stone, which did not have to be raised up the pyramid.

And that's another issue. How were the stones raised? Up some ramp, as is often widely assumed? If so, what slope would the ramp have had, and how many stones per hour were being hauled up this ramp at peak against the friction forces of wooden sledges being hauled over rough surfaces? Or, were the stones raised some other way, not involving the heavy workload of overcoming friction?

It turns out that these kinds of questions can be answered quite sensibly by simple calculations - not of the averaging kind above, but as follows:

• We know, by counting, how many tiers or courses of stone there are on a pyramid.
• So, knowing the shape of the pyramid and its base area, we can work out the volume of any tier. For the Great Pyramid, Akhet Khufu, (Khufu's Horizon) we know the base area is 230.33² multiplied by the tier height which we could either measure or assume to be 146.59 / 203, the number of tiers. (This is an approximation, of course, since the height of tiers tends to reduce with height, but it is usually good enough to get sensible results. Besides, not everyone counts the first tier, so the number could be 202, and the peak is missing - how many tiers would that have been?)
• Multiplying the volume of a tier by the density of limestone gives its mass, usually quoted in kilograms or tonnes, which can be converted to weight (in Newtons) simply be multiplying by g ( = 9.81ms^-2).
• We can then work out, using basic physics, the amount of work needed to raise the tier to its height above the surface, using the simple relation that work equals force times distance moved, where force is the weight of the tier, and distance is the height to which the tier has been raised
• Since the work was done by men, not machine, we know that the sole source of energy for doing all this work was the food that the men ate daily. We know what kinds of food they ate, and we can make a sensible estimate of their typical daily diet and calorific intake. From that, and a bit more physics, we can work out how much work, done in bursts, the typical man might have achieved per day
• Given the work needed to raise each tier, and the work output per man per day, we can calculate the man-days of work needed to raise each tier
• By assuming a manning strategy we can then work out the elapsed times needed to raise each tier. Manning strategies might include having a fixed number of men working on the pyramid, year-on-year, or recruiting as many men as are needed to raise one tier in a set time
• For Akhet Khufu, we are told that the overall time to raise the Pyramid was 20 years, so we can increase the food supply so that the sum of the days taken to raise each tier amounts to 20 years. This then tells us:
• How many men for each tier
• How long each tier took
• How much food and beer were needed
• How many ovens and vats would be needed and how many people would be needed to carry food and water, bake bread and brew beer.
• How many boats would be needed to supply the grain and water

The point of separating the calculations into tiers then, is that, instead of being stuck with averages, we can see how the building must have progressed over time. By using a simulation calculator, we can apply sensitivity checks, so that initial assumptions about times, levels of effort, diets, etc., can be varied separately and together to produce robust, statistically sound answers.

Cautionary Note

But, a word of caution. Using physics as a basis for working things out tends to provide an underestimate. There are so many things for which basic physics does not allow, e.g. waiting around time, supervision, organization, shift-working, etc. Additionally, physics would not be useful for working out the manpower involved in stone carving, polishing, etc.

Physics, then, since it results in an underestimate of manpower and effort, cannot prove any theories to be correct, but it can certainly prove some theories to be incorrect.

Work needed to Raise Great Pyramid, Tier-by-Tier

The figure shows some of the numerical values used in calculating the work associated with raising the Great Pyramid. The bulk of the stone was quarried on the Giza plateau, some 350m away and, while there may be doubts about a ramp on the Pyramid, it seems clear that a ramp was used to haul stone from the quarry to the base of the Pyramid.

The following graph shows the calculated work needed to raise each tier, measured in Joules.

There are 3 lines on the graph:-

1. The lowest line shows the work needed to raise each tier, assuming that the job was completed in 20 years and that no ramp was used - instead, as Herodotus was told, the builders used "contrivances made from short timbers". Note that the amount of work peaks at Tier 68. This is a feature of all pyramids. While there are many more stone per tier lower down, each stone has to be raised through only a short distance, so the work per stone is less. Conversely, higher up there may be less stones per tier, but the work per stone is greater because of the greater height through which they must be raised. The peak work per tier occurs at 1/3rd height, in this case Tier 68
2. The middle line shows the work per tier assuming that stones are hauled up ramps against the resistance of sliding friction
3. The upper line adds in the effects of quarrying the stone and of sliding it up the slope from the quarry

There was more to any pyramid complex than the pyramid. Additionally, calculations must account for:

• The Causeway up which stone and provisions would be hauled from the Nile to the pyramid complex site. According to Herodotus, the Causeway for Khufu's Pyramid took some 10 years to build - a massive undertaking
• The Valley Temple
• The Mortuary Temple, abutting on to the pyramid
• Queen's Pyramids and any ka pyramid
• Temenos wall surrounding the complex, together with any courtyards
• Boat Pits
• For 5th Dynasty pyramids, it would not be inappropriate to include the Sun Temples generally associated with them

The following graph shows the work needed for some of the features associated with Khufu.

The graph uses the tier number as the X-axis, rather than time in years. The amount of work per tier spent on the Causeway is a variable, since the calculator can be set to start and finish the Causeway; the area, representing the total Causeway work will remain constant.

Time Taken per Tier

There are many different ways of working out the numbers of men involved in working on the Great Pyramid. Already mentioned above are the different manning strategies, and these can have dramatic effects:

The graph above shows the time taken to raise each tier, including quarrying and hauling, but addressing the pyramid only, using two different manning strategies:-

1. The first manning strategy is to recruit as many men as needed at the time to raise the particular tier - this is called the proportional annual work force, since each year workers are recruited according to the work needed for that year. In the graph, this results in the horizontal line set at c.36 days per tier. You could work this out simply by dividing 20 years equally between 202 tiers. Of course, many more men would be needed in the early years to achieve this constant number of days per tier
2. The second manning strategy is to employ the same work force, year-on-year - this is called the constant annual workforce. This strategy results in lower tiers taking much longer - up to 69 days - simply because there are so many more stones to raise. The unexpected step at Tier 181 is due to the commencement of work on packing and casing the pyramid at that point

We do not know which, if either, strategy the architects used - it might have been neither, or a combination of the two. However, the building of the calculator raised the need to consider this and many other factors, often neglected.

One thought does militate against the constant annual workforce. As we have seen, the work needed to raise each tier peaks at 1/3rd the height. Using a constant annual workforce, it would appear to an observer that progress was slowing down as the pyramid started to rise. Perhaps this is why some pyramids were never finished, but were abandoned at less than 1/3rd height. Additionally, the builders had no idea how long their project would last, since they could not tell how long the pharaoh was going to live.

For all these reasons it seems sensible to presume that the architects would want to "front-load" the building programme by bringing in as many workers as they could recruit and use early on. This suggestion favours the proportional annual workforce manning strategy, especially for powerful pharaohs like Khufu who could, presumably, command however many men they wanted.

Numbers of Men Directly Employed in Hands-On Work

There are many different ways in which manpower can be calculated - we have just seen the effects of different manning strategies. On top of that, there is the so-called corvée, the annual recruitment of men from all over Egypt to help with pyramid building during the Inundation. The notion goes that the Inundation would render farmers along the Nile redundant until the floods receded; worse, the idle farmers might fall to squabbling. So, able-bodied farmers were recruited each year as a kind of national service, to help build the pyramid.

Nobody is absolutely certain that the corvée really occurred, but it seems like a reasonable idea, and current research is showing that the pyramid builders came from the south as well as the north of populated Egypt.

The calculator initially works out Full Time Equivalent Men (FTEM) per tier. One FTEM is one man working full time all year round. If the corvée took place for 3 months each year, then 4 men working for 3 months would, in principle, eat the same food and undertake the same work as one FTEM. And, just to confuse the issue, the manpower could be made up of a core team that did not change each year, plus a variable corvée chosen to make up the proportional annual workforce.

When the priests told Herodotus that up to 100,000 men worked on the Great Pyramid, were they exaggerating? Well, not necessarily. The graph shows the result of calculating the number of men needed to construct, not just the Great Pyramid, but the whole complex, employing the proportional manpower strategy, assuming that the corvée was in force, and calculating the numbers of men present on site during the Inundation. Remember, calculations based on physics must necessarily underestimate.

If we then remember, too, that supervision and organization have have not been accounted, and that shift-working might have been needed to cater for the harsh glare of the July and August sunshine, then we can easily top 60,000 men present on site, albeit only at the start beginning of the project, and only during the Inundation.

Rates of Setting Stone in Place

I mentioned at the start that one of the oft-quoted statistics about the Great Pyramid is that the rate of laying stone had to be 89 tonnes per hour, averaged out over 20 years - for the Pyramid alone, excluding the other features in the complex. The graph above shows that to be true. The blue line shows the Cumulative Rate of laying stone, in tonnes per hour, using the proportional manpower strategy. In effect, this tells you what the average would be if you calculated it any any time during the building programme. Right at the end, Tier 202, it does indeed come to 89 tonnes per hour.

Just how misleading this figure can be is shown by the black line, which shows the Mean Rate, also in tonnes per hour, of setting stone tier-by-tier, using proportional manpower. At the start, Tier 1, the figure reaches 264 tonnes per hour, before reducing down to less than 1 tonne per hour by Tier 196. (For the statistically minded, the blue line is effectively the running average.)

Rates of Setting Stone during Corvée

It gets worse. If, in any one year, you can calculate the mean tonnes per hour averaged out over the year, then it seems only reasonable to calculate how much of that was set during the corvée - after all, the point of having the corvée would be to make the greatest building progress.

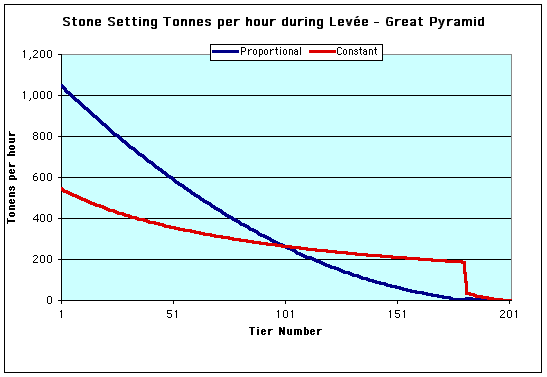
This graph shows the calculation, using the two manning strategies. With the proportional manpower strategy, the rate of setting stone could exceed 1000 tonnes per hour during the Inundation, but would rapidly tail off towards zero at higher tiers, since this strategy front-loads the work by bringing in many more men up front.

On the other hand, using the constant annual workforce (which could still have a corvée, but would employ the same numbers of men in the corvée each year) the rate of setting stone would not exceed 540 tonnes per hour during the Inundation. However, with no front loading, this constant annual workforce would have to maintain relatively high rates of setting stone at higher tier numbers, exceeding 187 tonnes per hour up to Tier 181. The sudden drop in rate of setting stone is caused by by the fixed workforce having to raise packing and casing stones at this time.

Parallel Pathways on Ramps

All this setting of tonnes of stone should raise concerns about ramps. Hollywood films may show shots of simple ramps winding around pyramids, but the amount of stone that ramps would have to carry seems excessive for a simple, temporary structure. If we make the usual assumption, that the average stone weighed 2.5 tonnes, then we can divide the Stone Setting Tonnes per hour from the previous graph by 2.5 to get the rate of stones being set per hour.

Imagine, if you will, stones being hauled up a ramp incline on sledges. Each team comprised some 25 men, most hauling on ropes, but some levering, some lubricating the sledge runners and at least one supervising. I estimate that one stone plus sledge, with ropes and men, would occupy about 33 linear metres on a ramp, and that there would need to be a space between successive stones and teams of another 33m to allow for each team hauling and resting, hauling and resting...as they climbed.

With this mental picture, the capacity of a single pathway on a single ramp going up a pyramid may be guestimated at some 2 stones per hour continuous. It could be less, it is unlikely to be much more. So, if we had to set stones in place on the pyramid at rates of tens or hundreds per hour, we would need multiple ramps and multiple pathways...

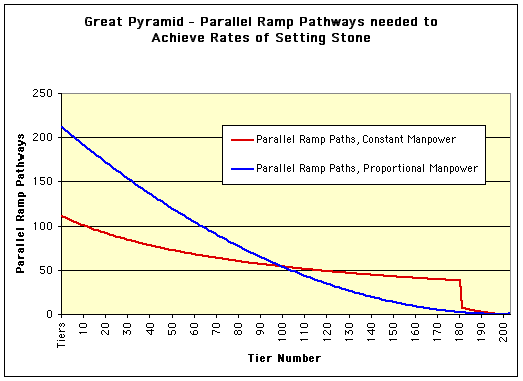
The graph shows the number of simultaneous/parallel paths needed, tier by tier for the two manning strategies. Lower down the pyramid, we are not talking so much about a nice, simple ramp, more a multi-lane highway of enormous proportions. Even if we presume, as some theorists do, that there would be 4 ramps, with 3 taking stone up, and one bringing men, ropes and sledges down, we are still into big numbers per ramp. Taking Tier 100, where the two manning strategy lines coincide, we would need 54 pathways, or 18 pathways per rising ramp. The constant manpower strategy would need some 38 parallel paths at Tier 180, at which height the amount of manoeuvring room has diminished to the point that many pundits doubt the credibility of even simple, single-path ramps.

On top of that, we have not considered the interruptions associated with continually extending the ramps and maintaining them as stone thundered up these supposedly temporary structures. You may have begun to see some cracks forming in the widely accepted ramp theory. You may think that, I couldn't possibly comment...

How long did it all take?

It is widely assumed that it took 20 years to build Khufu's Pyramid, and I have used that figure in the calculations above. However, one of the advantages of using a simulation calculator is that you can apply sensitivity checks to less certain figures. In the following analysis, I have combined sensitivity variations to 3 parameters, chosen because they are less certain that other figures used in the simulation:

1. The coefficient of friction between the sledge and whatever it is sliding over
2. The man-days taken to cut and dress each block of stone
3. The amount of work obtainable from each man per day

The graph shows the results of 100 runs, each estimating the build time with different values chosen for the 3 variables from their respective distributions. As the histogram shows, there is a decided spread of estimated years to build the Great Pyramid, with the bulk lying between 15 and 25 years.

The degree of variability is shown in the table, which suggests a more likely build time of some 24 to 25 years, but with a fair degree of uncertainty: it would be unreasonable to read too much into the analysis.

Conclusion

The Pyramid Calculator is a useful tool and, since it can be applied to any pyramid, it allows comparisons between pyramids to be made with relative ease. However, it does employ simply physics and mathematics, so it produces results which must be interpreted. For instance, it is unlikely that either of the two manning strategies above was employed precisely. Hemon, the architect, may have had other ideas, or his manning strategy might have been a compromise between the proportional and the constant manpower strategies. For all we know, there might have been fluctuations in available manpower according to the Inundation each year...

So, we should use the results from the calculations more as a rough guide than as hard and fast fact. Even then, I don't know about you but I'm a bit sceptical about those pyramid ramps...

Derek Hitchins

Last updated: Sept 2005

http://www.hitchins.net