Extracts from a new book,
"The Pyramid Builder's Handbook"
by
Derek K Hitchins©
Full copyright and intellectual property rights retained
Khufu's "Starshafts" Conform Much More Closely
to Prime Numbers than to Stars
The Star-shaft Theory
In a preceding section, we saw that the Great Pyramid incorporated 4 shafts, two emanating from the so-called Queen's Chamber and 2 emerging from the the King's Chamber. The shafts emerge horizontally from their respective chambers for a short distance before turning upwards at different slopes to point, supposedly, at four stars. Because of precession, the shafts do not point at any particular stars now, but by winding back the clock we get to a particular time, it is alleged, when the four shafts did indeed point at stars. That is not precisely true, however: the dates for accurately pointing at their respective stars do not tie up.
Take Thuban, for example:

The graph shows two lines:
- The horizontal line is the measured angle at which the northern shaft from the Queen'sChamber QC(N) points. That angle is constant, and is reasonably presumed to have been constant since building
- The rising line is the angle at which Thuban pointed over the years of the Old Kingdom, varying with the slow effects of precession
Where the two lines cross indicates the date, shown by the vertical dotted line, when the two angles coincide, i.e. when the shaft QC(N) pointed precisely at the star Thuban. It was 2350BC.

We can repeat that exerccise for each shaft. Plotting the four results gives this chart above, with plots and error bars for each shaft and associated star:
- KC(N) shaft pointed at Kocab in 2350BC - the same date as QC(N) and Thuban
- QC(S) pointed at Sirius in 2380BC
- KC(S) pointed at Alnitak in 2495BC
As the error bars suggest, these four dates do not appear to be consistent; in particular, the KC(S) shaft pointing at Alnitak is out on a limb.
So, what could these dates suggest?
- construction date - conventionally taken to be about 2566BC, off the chart to the top
- a slight misalignment in sighting - that would be uncharacteristic, and the shafts do appear to maintain their chosen slopes rather well
- some (then) future festivals, or
- absolutely nothing at all.
On top of that, we know that, although the upper shafts reach the outside of the pyramid, the lower ones do not. Rudolf Gantenbrik's discovery of a hidden chamber at the upper end of the QC(S) casts serious doubt on the purpose of that shaft, at least, being to point at any star. That discovery also put paid to the older idea that the shafts had been intended as ventilation, either for the deceased (?) or for the builders. If the shaft does not reach the outside, it clearly can be used neither for ventilation nor for star-spotting.
Overall, there are enough cracks and deviations in the so-called Star-shaft Theory for doubts to arise. The theory really is not being supported by the hard evidence of the ground. But, this theory once seemed so solid. Is there anay alternative theory?
Two Primes Interplay

Remembering that the ancient Egyptians used proportions to measure slopes, not angles as we do today, it seemed like a good idea to interpret the shaftslopes as proportions. The method and results are shown in the table. The second column shows the slope in degrees. The third column shows the tangent of that angle. Fourth and fifth columns show two numbers which, when divided give about the same ratio as the tangent, and the final column shows the error using this method in percent.
The results are astonishingly accurate. The shafts may not point very accurtely at their stars when they should, but they do conform to simple integer ratios with remarkable accuracy. The poorest accuracy, QC(S), equates to an error of only one part in 1000, while 0.0173 percent is less than 2 parts in 10,000 error!
Now, of course, this could be just fortuitous - simple chance. However, it does not end there.
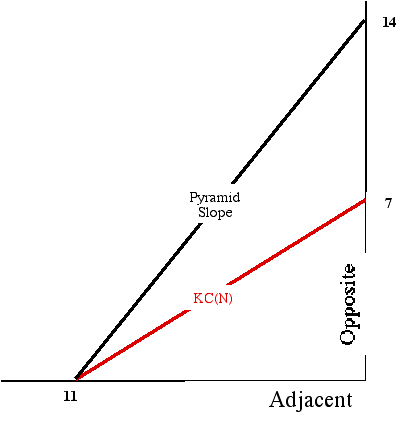
Consider just KC(N) for a moment. Its slope is given by 7:11, while the slope of the Great Pyramid is given by 14:11. Now, if you use proportions to determine slope, then one of these slopes is exactly half the other. Measuring in the ancient Egyptian unit for slope, the seked, reinforces the issue:
- 7:11 is 11 seked
- 14:11 is 5 1/2 seked.
(Note, using seked results in a larger number for a smaller incline.)
So, in their terms, KC(N) neatly, precisely and symmetrically divides Khufu's slope in two. If KC(N) was intended to point to the, then, Pole Star or Great Mooring Post, then this would tie the slope of Khufu's Pyramid to the elevation of Thuban.
This provides an explanation for the pointing direction of one shaft, but more importantly it explains why the dimensions of the Great Pyramid are in the ratio of 14:11 - nothing to do with pi, everything to do with access to the only stationary point in the heavens - the Great Mooring Post.
There's more:
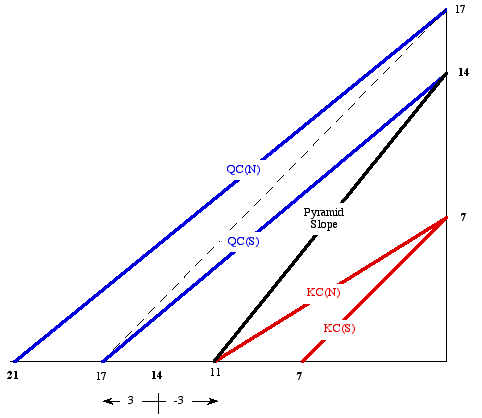
The figure shows all the shafts and the Pyramid slope plotted out on x-y co-ordinates. A pattern is evident, since 7, 14 and 21 recur, and 11 and 17 are 14 plus and minus 3.
It is known that ancient mathematicians, including the Greeks, were fascinated by prime numbers. Such is not known about the ancient Egyptians - so far. However, a simple "2-Primes Interplay" is now evident in the numbers, as follows, where the 2 primes are 3 and 7:
7 = 1 x 7
11 = 2 x 7 - 3
14 = 2 x 7
17 = 2 x 7 + 3
21 = 3 x 7
So, if the 2-Primes Interplay Theory is correct, just what were the ancient Egyptians up to with their 4 shafts? One explanation would be that they were up to "number magic". Numbers, particularly some numbers, were believed to have great magical powers, and it may be that the architects of the Old Kingdom were creating a structure which incorporated a set of magic prime numbers to give power to the King's Resurrection Machine, and to tie it in some way to the heavens so ensuring his continued reign after death, and hence the continued fertility of Egypt.
Does the 2-Primes Interplay Theory invalidate the starshaft theory? Judge for yourself. The evidence does not really support the starpointing idea with any accuracy, but the evidence does support the 2-Primes Interplay with phenomenal accuracy. Me? I like the starshaft idea, but I go with the evidence.